Description
August 1, 2019The data/codes presented here is published in [1]. Using the data, we will show how to perform heat diffusion on surface mesh by performing three different polynomial approximation. The codes have been tested with iMac with MATLAB 2016. If you are using the dataset or codes, please reference [1]. The complete package is zipped into matlab.zip. The package will show how to perform heat diffusion on surface mesh coordinates by the polynomial approximation of the Laplace-Beltrami operator in EXAMPLE.m. The package consists of three functions heat_chebyshev.m, heat_hermite.m, heat_laguerre.m each corresponding to Chebyshev, Hermite and Lagurre polynomial approximations. Figure 1 shows examples the surface mesh smoothing.
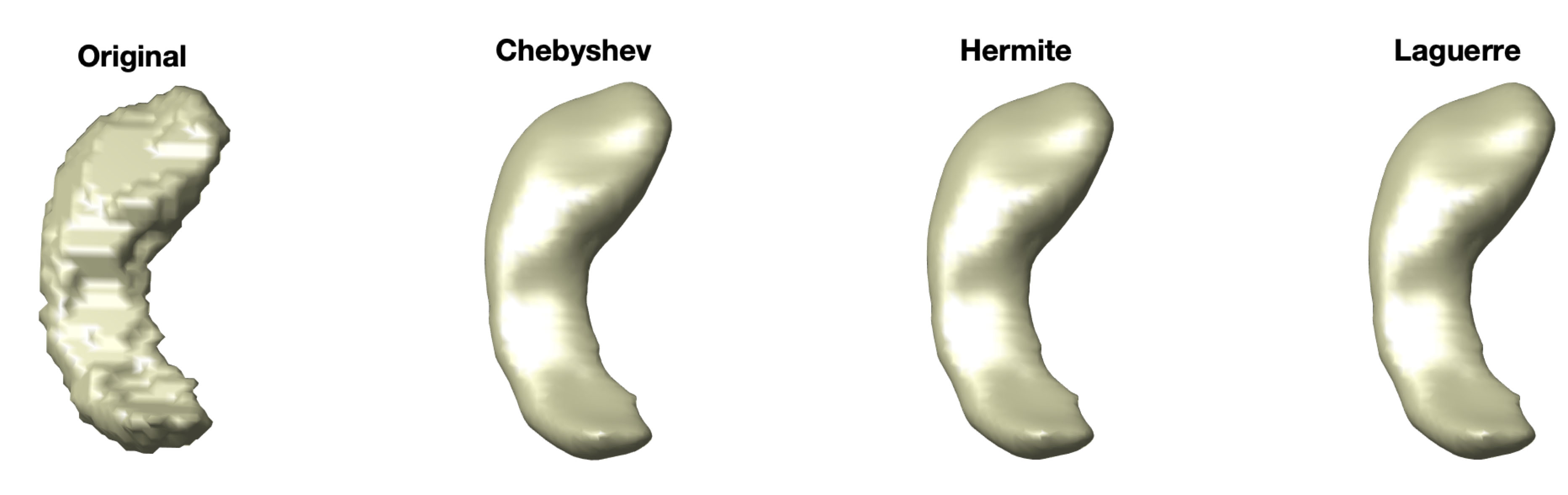
Figure 1. Diffusion of the surface coordinates of a hippocampus using three different polynomial approximations.
Polynomial approximation of Laplace-Beltrami
operator
August 1, 2019The method is based on approximating the Laplace-Beltrami operator via polynomial approximations. The Chebyshev polynomial approximation was used in building the diffusion wavelet [2]. We generalized the method to Hermite and Lagurre polynomial approximations in solving heat diffusion for the first time [1]. The EXAMPLE.m will generate the hippocampus example (Figure 1) in [1] and computes the reconstruction error (Figure 2).
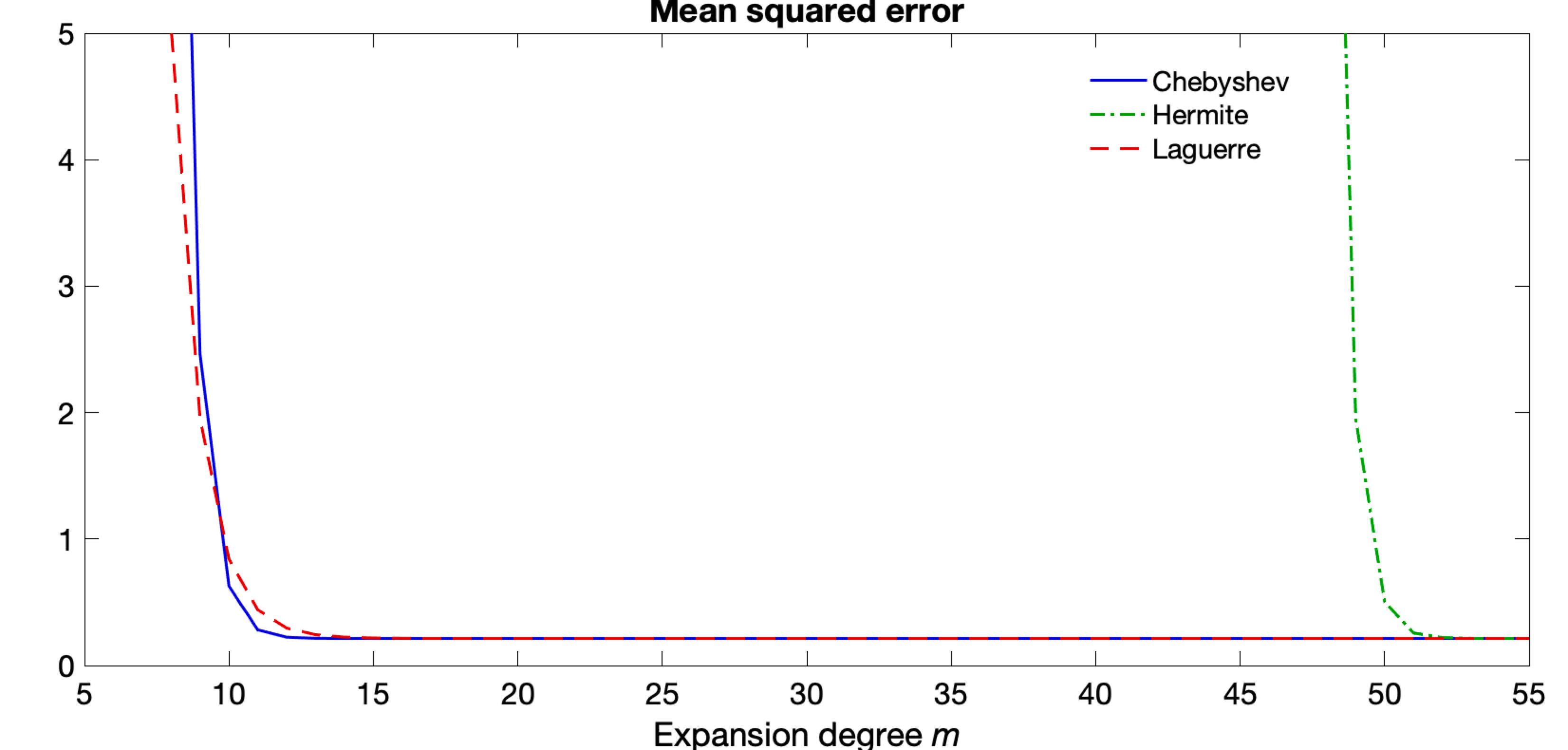
Figure 2. Reconstruction error
of the three methods. Chebyshev and Laguerre
polynomials perform the best while Hermite
polynomials does not converge fast enough.
Reference
[1] Huang, S.-G., Lyu, I., Qiu, A., Chung, M.K. 2019 Fast polynomial approximation to heat diffusion in manifolds, Medical Image Computing and Computer Assisted Intervention (MICCAI)
[2] Tan, M., Qiu, A. 2015, Spectral Laplace-Beltrami wavelets with applications in medical images. IEEE Transactions on Medical Imaging 34, 1005-1017, 2015