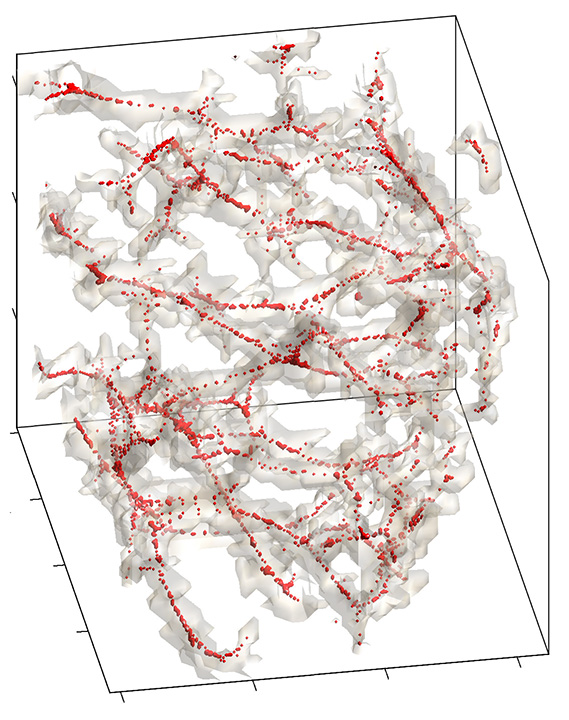
Skeleton representation of lung blood vessel tree obtained from CT. Students will learn advanced  data and image representation and visualization techniques as well as quantification methods used in medical image processing and analysis. Read book chapter Chung et al. 2018 for more detail on the vessel tree modeling.