HW02: Practice with logistic regression and decision tree

[Please put your name and NetID here.]

Hello Students:

• Start by downloading HW02.ipynb from this folder. Then develop it into your solution.

• Write code where you see "... your code here ..." below. (You are welcome to use more than one cell.)

• If you have questions, please ask them in class or office hours. Our TA and I are very happy to help with the programming (provided you start early enough, and provided we are not helping so much that we undermine your learning).

• When you are done, run these Notebook commands:

  • Shift-L (once, so that line numbers are visible)
  • Kernel > Restart and Run All (run all cells from scratch)
  • Esc S (save)
  • File > Download as > HTML

• Turn in HW02.ipynb and HW02.html to Canvas's HW02 assignment (use 'Add A File')

  As a check, download your files from Canvas to a new 'junk' folder. Try 'Kernel > Restart and Run All' on the '.ipynb' file to make sure it works. Glance through the '.html' file.

• Turn in partial solutions to Canvas before the deadline. e.g. Turn in part 1, then parts 1 and 2, then your whole solution. That way we can award partial credit even if you miss the deadline. We will grade your last submission before the deadline.

# ... your code here ... (import statements)

1. Logistic regression

1a. Make a logistic regression model

relating the probability an iris has Species='virginica' to its 'Petal.Length' and classifying irises as 'virginica' or not 'virginica' (i.e. 'versicolor').

• Read http://www.stat.wisc.edu/~jgillett/451/data/iris.csv into a DataFrame.
• Make a second data frame that excludes the 'setosa' rows (leaving the 'virginica' and 'versicolor' rows) and includes only the Petal.Length and Species columns.
• Use linear_model.LogisticRegression(C=1000) so we all get the same results (they vary with C).
• Train the model using $X=$ petal length and $y=$ whether the Species is 'virginica'. (I used "y = (df['Species'] == 'virginica').to_numpy().astype(int)", which sets y to zeros and ones.)
• Report its accuracy on the training data.
• Report the estimated P(Species=virginica | Petal.Length=5).
• Report the predicited Species ('virginica' or 'versicolor') for Petal.Length=5.
• Make a plot showing:
  • the data points
  • the estimated logistic curve
  • and what I have called the "sample proportion" of y == 1 at each unique Petal.Length value
  • a legend and title and other labels necessary to make the plot easy to read

# ... your code here ...

1b. Do some work with logistic regression by hand.

Consider the logistic regression model, $P(y _i = 1) = \frac{1}{1 + e^{-(\mathbf{w x} + b)}}\,.$

Logistic regression is named after the log-odds of success, $\ln \frac{p}{1 - p}$, where $p = P(y_i = 1)$. Show that this log-odds equals $\mathbf{w x} + b$. (That is, start with $\ln \frac{p}{1 - p}$ and connect it in a series of equalities to $\mathbf{w x} + b$.)

... your Latex math in a Markdown cell here ...

$\begin{align*} % In this Latex context, "&" separates columns and "\\" ends a line. \ln \frac{p}{1 - p} & = ...\\ & = ...\\ & = ...\\ & = ...\\ & = \mathbf{w x} + b\\ \end{align*} $

1c. Do some more work with logistic regression by hand.

I ran some Python/scikit-learn code to make the model pictured here: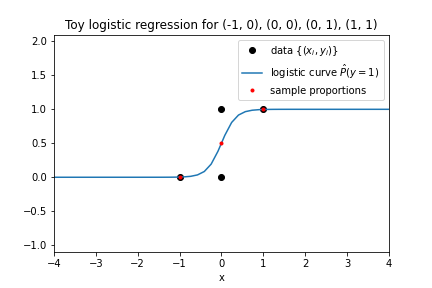

From the image and without the help of running code, match each code line from the top list with its output from the bottom list.

1. model.intercept_
2. model.coef_
3. model.predict(X)
4. model.predict_proba(X)[:, 1]

A. array([0, 0, 0, 1]), B. array([0.003, 0.5, 0.5, 0.997]), C. array([5.832]), D. array([0.])

# ... Your answer here in a Markdown cell ...
# For example, "1: A, 2: B, 3: C, 4: D" is wrong but has the right format.

2. Decision tree

2a. Make a decision tree model on a Titanic data set.

Read the data from http://www.stat.wisc.edu/~jgillett/451/data/kaggle_titanic_train.csv.

These data are described at https://www.kaggle.com/competitions/titanic/data (click on the small down-arrow to see the "Data Dictionary"), which is where they are from.

• Retain only the Survived, Pclass, Sex, and Age columns.
• Display the first seven rows (passengers). Notice that the Age column includes NaN, indicating a missing value.
• Drop rows with missing data via df.dropna(). Display your data frame's shape before and after dropping rows. (It should be (714, 4) after dropping rows.)
• Add a column called 'Female' that indicates whether a passenger is Female. You can make this column via df.Sex == 'female'. This gives bool values True and False, which are interpreted as 1 and 0 when used in an arithmetic context.
• Train a decision tree with max_depth=None to decided whether a passenger Survived from the other three columns. Report its accuracy (with 3 decimal places) on training data along with the tree's depth (which is available in clf.tree_.max_depth).
• Train another tree with max_depth=2. Report its accuracy (with 3 decimal places). Use tree.plot_tree() to display it, including feature_names to make the tree easy to read.

# ... your code here ...

2b. Which features are used in the (max_depth=2) decision-making? Answer in a markdown cell.

# ... your English text in a Markdown cell here ...

2c. What proportion (in the cleaned-up data) of females survived? What proportion of males survived?

Answer in two sentences via print(), with each proportion rounded to three decimal places.

Hint: There are many ways to do this. One quick way is to find the average of the Survived column for each subset.

# ... your code here ...

2d. Do some decision tree calculations by hand.

Consider a decision tree node containing the following set of examples $S = \{(\mathbf{x}, y)\}$ where $\mathbf{x} = (x_1, x_2)$:

((4, 9), 1)

((2, 6), 0)

((5, 7), 0)

((3, 8), 1)

Find the entropy of $S$.

# ... your brief work and answer here in a markdown cell ...

2e. Do some more decision tree calculations by hand.

Find a (feature, threshold) pair that yields the best split for this node.

# ... your brief work and answer here in a markdown cell ...