Diffusion Smoothing on the Cortical Surface
Moo K. Chung , Keith J. Worsley
, Keith J. Worsley
 ,
Jonathan Taylor
,
Jonathan Taylor ,
Jim Ramsay
,
Jim Ramsay ,
Steve Robbins
,
Steve Robbins ,
Alan C. Evans
,
Alan C. Evans
 Department
of
Mathematics and Statistics
Department
of
Mathematics and Statistics
 Montreal
Neurological
Institute
Montreal
Neurological
Institute
 Department
of
Psychology, McGill University
Abstract
Department
of
Psychology, McGill University
Abstract
Gaussian kernel smoothing has been widely used in either 2D flat or
3D
volume images, but it does not work on the curved cortical surface.
However, by reformulating Gaussian kernel smoothing as a solution to
a
diffusion equation on a 2D manifold, we can generalize it to the
cortical surface. This generalization is called diffusion
smoothing
and has been used in analysis of fMRI data on the cortical surface
[1]
and detecting cortical surface-area growth [3]. We give an exact
mathematical formulation for the diffusion smoothing on triangulated
cortical surfaces so that this technique can be used for any
surface-based functional and structural analysis. As an
illustration,
we smooth the mean curvatures on the outer cortical surfaces to show
how the the smoothing actually incorporates the geodesic curvature
information of the surface.
 |
|
| Figure 1: A typical triangulation |
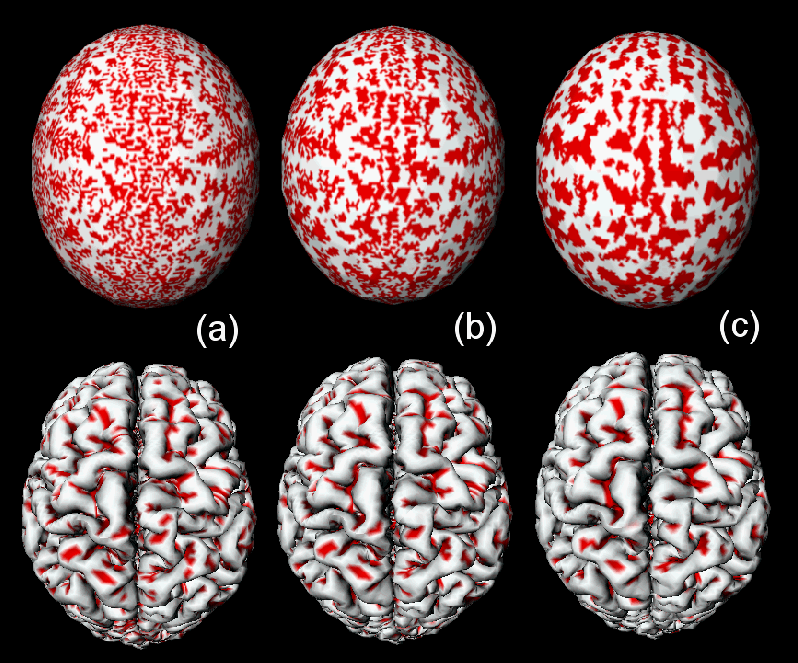
Figure 2: The mean curvature
from the outer cortex is mapped onto an ellipsoid during the
diffusion
smoothing. (a) Before the iteration (b) After 40 iterations
(c) After
100 iterations |
Methods
Gaussian kernel smoothing of the signal f(x) in
n-dimension with
FWHM=4(ln2)1/2t1/2 is defined as the
convolution of the n-dimensional Gaussian kernel G(x;t)
with the
signal f(x), i.e. F(x,t)=f*G(x;t). It can be shown
that
the convoluted signal F is the solution of a diffusion
equation dF/dt=L[F]
with the n-dimensional Euclidean Laplacian L. Since the
cortical
surface in non-Euclidean, the Euclidean Laplacian is not well
defined on
the cortical surface. The generalization of the Laplace operator L
to an arbitrary curved surface is called the Laplace-Beltrami
operator and it is defined in terms of the Riemmanian metric
tensors.
In order to estimate the Laplace-Beltrami operator on a
triangulated
cortical surface, we have used the finite element method[2].
Let F(pi)
be the signal on the i-th node pi in
the
triangulation. If p1,...,pm are m-neighboring
nodes
around p=p0, the Laplace-Beltrami operator at p
is estimated by
L[F(p)]=w1(F(p1)-F(p)) +...+wm(F(pm)-F(p))
with the weights wi=(cot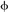 i+cot
i+cot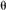 i)/(T1+...+Tm),
where
i)/(T1+...+Tm),
where 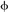 i
and
i
and 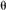 i
are the two angles opposite to the edge pi-p in
triangles and T1+...+Tm is
the sum
of the areas of m-incident triangles at p (Figure
1).
Then the diffusion equation is solved via the finite
difference
scheme:
i
are the two angles opposite to the edge pi-p in
triangles and T1+...+Tm is
the sum
of the areas of m-incident triangles at p (Figure
1).
Then the diffusion equation is solved via the finite
difference
scheme:
F(pi,tn+1)=F(pi,tn)+(tn+1-tn)L[F(pi,tn)]
with the initial condition F(pi,t0)=f(pi).
After N-iterations, the diffused signal is locally
equivalent
to the Gaussian kernel smoothing with FWHM=4(ln2)1/2N1/2(tn-t0)1/2
[2].
Results
The ASP method [3] is used to extract the outer cortical surfaces
each
consisting of 81920 triangles from MR scans. At this surface
sampling
rate, the average intervertex distance is about 4mm. The mean
curvature f(pi)
of the cortical surface is computed based on the least-squares
estimation of a local quadratic surface [2]. Figure 2 shows the
diffusion smoothing of the mean curvature with 5mm FWHM. If the
smoothing were based on simple inter-nodal averaging, such sulcal
pattern is not possible to obtain.
Conclusion
Gaussian kernel smoothing can be generalized to cortical surfaces
enabling surface-based statistical analysis. The numerical
implementation will be freely available as Matlab code on the web
at
http://www.math.mcgill.ca/keith/BICstat.
References
[1] Andrade A et al., Detection of fMRI Activation on the
Cortical
Surface, NeuroImage, 2000 (in press).
[2] Chung MK et al.,
http://www.math.mcgill.ca/chung/diffusion/diffusion.pdf, 2000
[3] Chung MK et al., Statistical Analysis of Cortical Surface Area
Change, with an Application to Brain Growth, HBM2001 Conference
[4] MacDonald D et al., NeuroImage 12:340-356, 2000
 , Keith J. Worsley
, Keith J. Worsley
 ,
Jonathan Taylor
,
Jonathan Taylor ,
Jim Ramsay
,
Jim Ramsay ,
Steve Robbins
,
Steve Robbins ,
Alan C. Evans
,
Alan C. Evans
 Department
of
Mathematics and Statistics
Department
of
Mathematics and Statistics  Montreal
Neurological
Institute
Montreal
Neurological
Institute  Department
of
Psychology, McGill University
Department
of
Psychology, McGill University

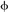 i+cot
i+cot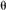 i)/(T1+...+Tm),
where
i)/(T1+...+Tm),
where