Tensor-Based Surface Morphometry applied to Gray Matter Maturation
Moo K. Chung
 ,
Keith J. Worsley
,
Keith J. Worsley
 ,
Tomas Paus
,
Tomas Paus , Steve Robbins
, Steve Robbins ,
Jonathan Taylor1, Jay N. Giedd
,
Jonathan Taylor1, Jay N. Giedd 2,
Judith L. Rapoport
2,
Judith L. Rapoport 2,
Alan C. Evans
2,
Alan C. Evans
 Department of Statistics
Department of Statistics
 W.M. Keck laboratory
for functional brain imaging and behavior, University of Wisconsin-Madison
W.M. Keck laboratory
for functional brain imaging and behavior, University of Wisconsin-Madison
 Department of
Mathematics and Statistics
Department of
Mathematics and Statistics
 Montreal Neurological
Institue, McGill University
Montreal Neurological
Institue, McGill University
1Department of Statistics, Stanford University
2Child Psychiatry Branch, National Institute of Mental
Health
Abstract
We present tensor-based surface morthometry that does not require the
regions of interest (ROI) and apply it to the problem of quantifying the
gray matter growth patterns for 28 children and young adults aged between
12 and 16. The gray matter has the topology of a 2D highly convoluted thin
sheet. As the brain develops over time, the cortical surface area, thickness,
curvature and total gray matter volume change. It is highly likely that
such age-related surface deformations are not uniform. By measuring how
such surface metrics change over time, the regions of the most rapid structural
changes can be detected.
Methods
We used anatomic segmentation using proximities (ASP) method (McDonalds
et al, 2001) to generate both outer and inner surface meshes from classified
MRIs. Then the surface meshes were parameterized by local quadratic polynomials
(Chung et al, 2002). The cortical surface deformaion was modeled as the
boundary of ulticomponent fluids (Drew, 1991). Using the same stochastic
assumption on the deformation field used in Chung et al. (2001), the distributions
of area dilatation rate, cortical thickness and curvature changes can be
derived. To increase the signal to noise ratio, diffusion smoothing (Andrade
,2001; Chung et al., 2002) has been developed and applied to surface data.
surfaceThe diffusion smoothing algorithm written in Matlab is freely available
at http://www.stat.wisc.edu/~mchung.
Afterwards, statistical inference on the cortical surface is performed
via random fields theory (Worsley et al., 1994).
Results and discussion
It is found that the cortical surface area and gray matter volume shrinks,
while the cortical thickness and curvature tends to increase between ages
12 and 16 with a highly localized area of cortical thickening and surface
area shrinking found in the superior frontal sulcus at the same time. It
seems that the increase in thickness and decrease in the superior frontal
sulcus area are causing incresed foldings in the middle and superior frontal
gyri (see the figure).
Because our technique is based on cordinate-invariant tensor geometry,
artificial surface flattening (Andrade et al.,B 2001; Angenent et al.,
1999), which can destroy the inherent geometrical structures of the cortical
surface, has been avoided.
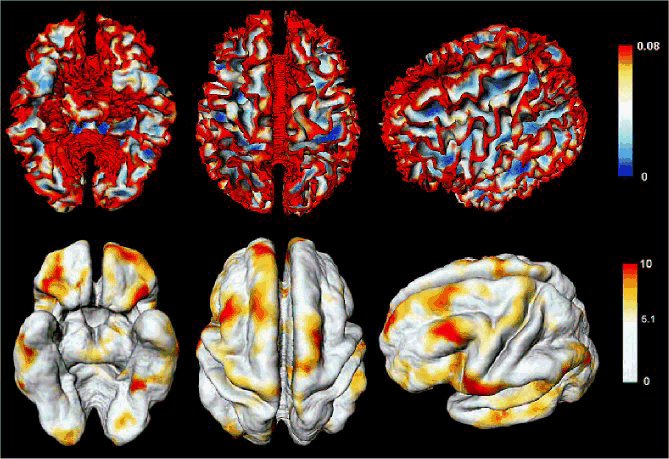 |
| Top: Bending energy computed on the inner cortical surface
of a 14 year old subject. Bottom: t map showing the regions of curvature
increase. Most of curvature increase occurs on gyri. |
References
Andrade, A., Kherif, F., Mangin, J., Worsley, K.J., Paradis, A., Simons,
O., Dehaene, S., Le Bihan, D., Poline J-B. (2001) Detection of fMRI activation
using cortical surface mapping, Human Brain Mapping, 12:79-93.
Chung, M.K., Worsley, K.J., Paus, T., Cherif, D.L., Collins, C., Giedd
J., Rapoport, J.L., Evans, A.C. (2001) A unified statistical approach to
deformation-based morphometry, NeuroImage, 14:595-606.
Chung, M.K., Worsley, K.J., Paus, T., Robbins, S., Taylor, J. Giedd,
J.N., Rapoport, J.L., Evans, A.C. (2002) Tensor-based surface morphometry,
Department TR 1049. http://www.stat.wisc.edu/~mchung.
Drew, D.A. (1991) Theory of multicomponent fluids, Springer-Verlag,
New York.
MacDonalds, J.D., Kabani, N., Avis, D., Evans, A.C. (2001) Automated
3-D extraction of inner and outer surfaces of cerebral cortex from MRI,
NeuroImage, 12:340-356.
Worsley, K.J., Marrett, S., Neelin, P., Vandal, A.C., Friston, K.J.,
Evans, A.C. (1996) A unified statistical approach for determining significant
signals in images of cerebral activation, Human Brain Mapping, 4:58-73.

 ,
Keith J. Worsley
,
Keith J. Worsley
 ,
Tomas Paus
,
Tomas Paus , Steve Robbins
, Steve Robbins ,
Jonathan Taylor1, Jay N. Giedd
,
Jonathan Taylor1, Jay N. Giedd 2,
Judith L. Rapoport
2,
Judith L. Rapoport 2,
Alan C. Evans
2,
Alan C. Evans
 Department of Statistics
Department of Statistics
 W.M. Keck laboratory
for functional brain imaging and behavior, University of Wisconsin-Madison
W.M. Keck laboratory
for functional brain imaging and behavior, University of Wisconsin-Madison
 Department of
Mathematics and Statistics
Department of
Mathematics and Statistics
 Montreal Neurological
Institue, McGill University
Montreal Neurological
Institue, McGill University
