
 ,
Andrew L. Alexander
,
Andrew L. Alexander
 ,
Yuefeng Lu
,
Yuefeng Lu

 Department of Statistics
Department of Statistics
 Departmnet of
Biostatistics and Medical Informatics
Departmnet of
Biostatistics and Medical Informatics
 W.M. Keck Laboratory
for Functional Brain Imaging and Behavior
W.M. Keck Laboratory
for Functional Brain Imaging and Behavior
 Department of Medical
Physics, University of Wisconsin-Madison
Department of Medical
Physics, University of Wisconsin-Madison
 ,
Andrew L. Alexander
,
Andrew L. Alexander
 ,
Yuefeng Lu
,
Yuefeng Lu

 Department of Statistics
Department of Statistics
 Departmnet of
Biostatistics and Medical Informatics
Departmnet of
Biostatistics and Medical Informatics
 W.M. Keck Laboratory
for Functional Brain Imaging and Behavior
W.M. Keck Laboratory
for Functional Brain Imaging and Behavior
 Department of Medical
Physics, University of Wisconsin-Madison
Department of Medical
Physics, University of Wisconsin-MadisonAnisotropic Smoothing
Anisotropic Gaussian kernel K(x) with bandwidth matrix
H is given as a mean zero multivariate normal probability density
function with HH' as the covariance matrix. Then the anisotropic
kernel smoothing of signal f(x) is defined as the convolution
F(x) = K*f(x). One simple way to match
the covariance matrix to the diffusion tensor D in such a way that
the signal would be smoothed along the white fiber track is by letting
HH'=2tD, where t is the scaling parameter. Discretizing the
convolution, we have a discrete Gaussian kernel smoothing F(x)
= 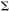 wj(x-xj)f(xj),
where the summation is taken over the neighboring voxels around x
and wj are positive weights that sum to 1. The scaling
parameter t controls the amount of smoothing and isotropy. As t
increases, the smoothing and isotropy increase.
wj(x-xj)f(xj),
where the summation is taken over the neighboring voxels around x
and wj are positive weights that sum to 1. The scaling
parameter t controls the amount of smoothing and isotropy. As t
increases, the smoothing and isotropy increase.
Connection Probability
As an application of the above anisotropic Gaussian kernel smoothing,
we show how to represent and compute the connection probability along the
white fiber tracks. The probability of going from p to q
under diffusion is P(p,q)=K(q-p)
when p and q are very close (Stevens, 1995). The probability
of going from p to any q is the sum of the probabilities
of going from p to q through all possible intermediate points
x. Then it can be shown that the approximate connection probability
between p and q is given by P(p,q)=
K*P(p,q), where the convolution is taken over
the first argument of P. Hence the connection probability is given
as an iterative integral equation with the initial condition P(p,p)=1.
A similar discretization gives P(p,q)= 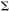 wj(p-xj)P(xj,q),
where the summation is taken around the neighboring voxels of p.
wj(p-xj)P(xj,q),
where the summation is taken around the neighboring voxels of p.
To generate the connection probability map from a given p, we iteratively apply anisotropic kernel smoothing Fn+1(x)=K*Fn(x) with the initial condition F0(x)=1 if x=p and 0 otherwise (Chung et al., 2003). The iteration is repeated until it hits q. Our formulation is analogous to the diffusion equation approach: dF/dt = div(D grad F) with initial condition F(x,0)= 1 if x=p and 0 otherwise (Batchelor et al., 2001). However, our solution is not exactly the solution of the above diffusion equation although the resulting connection probability maps are quite similar. Compared to solving the diffusion equation, our approach is extremely fast.
References
Batchelor, P.G., Derek L.G.H., Calamante, F., Atkinson, D. (2001) Study
of Connectivity in the Brain Using the Full Diffusion Tensor from MRI.
IPMI 2001: 121-133.
Chung, M.K., Alexander, A.L., Lu, Y. (2003). Probabilistic representations of connectivity information in diffusion tensor imaging, TR Department of Statistics, University of Wisconsin-Madison. http://www.stat.wisc.edu/~mchung/papers/DTI_tech.pdf
Stevens, C.F. (1995). The six core theories of modern physics, The MIT Press.