|
|
Nonparametric estimation of cortical
thickness |
Moo K. Chung1,2,3 ,
Shijie Tang,1
1Department of Statistics, 2Department of Biotatistics and
Medical Informatics, 3Keck
Laboratory for Functional Brain Imaging and Behavior,
University of Wisconsin-Madison
|
Abstract
The cerebral cortex
has the topology of a 2D highly convoluted sheet. The cortical
thickness that measures the distance between the outer and
inner cortical surfaces has been used to characterize the
brain shape [1]. There are many different techniques to
measure the cortical thickness [1, 2, 3, 4]. Which method one
uses, the thickness measurements are always contaminated with
noise. The noise may come from a scanner or due to partial
volume effect. To increase the signal-to-noise ratio and to
increase Gausianess that is needed in the random fields
theory, diffusion smoothing has been used so far [1]. We
present a completely new smoothing technique that is simpler
than diffusion smoothing.
Methods
T1 weighted
MRIs are segmented and cortical thickness maps are computed
based on deformable surface algorithm presented in [2] using
FreeSurfer package. The triangular mesh generated in this way
has about 300,000 triangle elements in average, which is the
sufficient mesh resolution for 1mm resolution MRI obtained
from 3T GE scanner. The cortical thickness measurement is
assumed to follow the additive model of true signal plus
noise. The true cortical thickness is assumed to be a
continuous functional data that can be estimated via the
Nadaraya-Waton (NW) smoother. The NW kernel smoothing is
essentially a Gaussian kernel smoothing for sparse data. The
amount of smoothing can be increased by iteratively applying
NW kernel smoothing.
Results
Single iteration
of Gaussian kernel smoothing takes about 1 min in Pentium
M-processor machine which is compatible to the speed of
diffusion smoothing. Figure 1 is the cortical thickness
measurements obtained from FreeSurfer and Figure 2 is the NW
kernel estimation of the thickness measure which shows huge
reduction of noise. Figure 3 is the local comparison of the
thickness maps before and after smoothing. The thickness maps
are deformed onto a sphere to show hidden sulcal regions.
Figure 4 is an application of the NW kernel estimation for
smoothing out noisy brain surface. To show the effect of
surface regularization, artificially large white noise has
been added to the coordinates of the mesh.
Acknowledgments
This work was funded by
WARF. The authors wish to thank Bruce Fischl and his research
staff for valuable advice on segmentation.
[1] Chung,
M.K., Worsley, K.J., Robbins, S., Paus, P., Taylor, J., Giedd,
J.N., Rapoport, J.L., Evans, A.C. (2003) Deformation-Based
Surface Morphometry with an Application to Gray Matter
Deformation, NeuroImage. 18:198-213.
[2] Fischl, B. and
Dale, A.M. (2000) Measuring the thickness of the human
cerebral cortex from magnetic resonance images, PNAS
97:11050-11055.
[3] Jones, et al. (2000) Three-dimensional
mapping of cortical thickness using Laplace’s equation, Human
Brain Mapping 11:12-32.
[4] Miller, M.I. et al. (2000)
Bayesian construction of geometrically based cortical
thickness metrics. NeuroImage.
12:676-687.
|
|
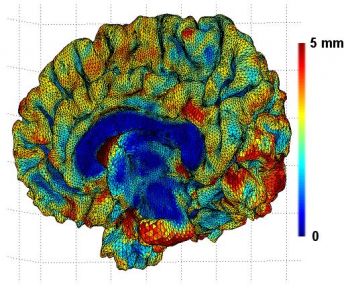
Figure 1. Cortical thickness
measurement
|
|
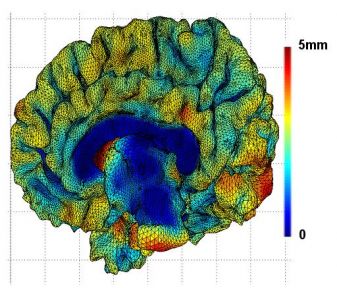
Figure 2. Cortical thickness
estimation
|
|
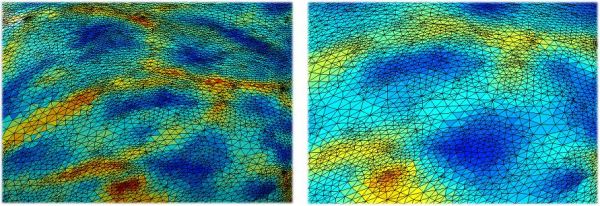
Figure 3. Comparision of before and
after smoothing
|
|
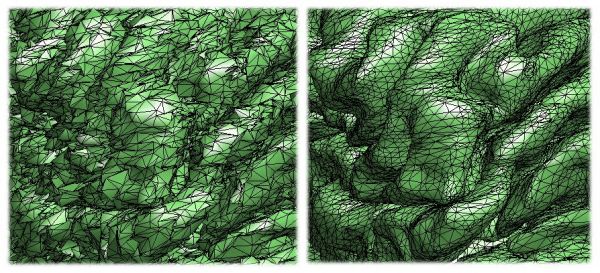
Figure 4. Nonparametric estimation of
noise brain surface
|
|
|