|
Subpixel curvature estimation of the corpus
callosum via splines and its application to autism
|
Thomas J. Hoffmann1
, Moo K. Chung,1,2,3 , Kim M. Dalton,3 , Andrew L. Alexander,3,4,5
, Grace Wahba,1,2 , Richard J.
Davidson,3,4,6
1Department of
Statistics, 2Department of
Biotatistics and Medical Informatics, 3Keck
Laboratory for Functional Brain Imaging and Behavior, 4Department
of Psychiatry, 5Department of Medical
Physics, 6Department of Psychology,
University of Wisconsin-Madison
|
Abstract
Autism is a neurodevelopmental disorder with abnormal corpus callosum
(CC) size [1]. Most previous studies used the area of predefined
Witelson partition [5] as a morphometric measure but other shape
metrics have not been considered. We present a novel computational
technique for curvature estimation via piecewise quintic splines and
use it in both CC nonlinear dynamic time warping algorithm [4] and
detecting the regions of curvature difference.
Methods
A group of 2D mid sagittal cross section images of the corpus callosum
was taken from males of similar age, 15 autistic, and 12 normal
controls. The level set method as described by Sethian[2], was used to
extract the outline of the corpus callosum automatically. Thus the
pixelated CC contour was reconstructed into a rough closed curve in
Euclidean space (Figure 1. red). Smoothing of this zigzag contour was
necessary to account for the partial volume effect (Figure 1. blue).
Two different methods were used to smooth and estimate the curvature
function. The first method uses Taubin's smoothing [3], a Gaussian
filtering without shrinkage, followed by the least-squares estimation.
The second method uses a series of quintic splines to estimate the
first and second derivatives to compute the curvature. Afterwards a
curve from the control group was chosen as a template and all other
curves are registered to the template. First an affine registration was
used to normalize the global CC size differences. Second the fast
nonlinear dynamic-time warping algorithm was used [4]. The algorithm
penalized against large deformation and curvature difference, thereby
matching the extrema of curvature while maintaining a smooth and stable
deformation. After registering the curves, a local estimation of
curvature could be compared across subjects, using Welch's t-test at
each point to correct for the somewhat unequal variance in a few areas
(Figure 3).
Results
Both methods provided effective estimates of curvature for the entire
CC contours. The smoothing splines performed better in terms of ease of
fit and more stable results. The results of the comparison of
curvatures between the autistic and control subjects are as shown in
Figure 2 where the sample mean curvature functions are plotted (blue:
autistic, red: control). Figure 4 is the P-value map where the blue
areas indicate more significant curvature difference. Most significant
curvature difference is detected at the posterior midbody (R1).
Acknowledgements
The original level set and dynamic time warping code were obtained from
Fan Ding and Yuefeng Lu and have been modified extensively. This work
was funded by WARF, NIMH U54 MH066398-1A1, NSF Grant DMS0072292 and by
a NARSAD Distinguished Investigator Award to RJD.
References
[1] Harden, A.Y. et al. Corpus Callosum Size in Autism.
Neurology, 55:1033-1036, 2000.
[2] Malladi, R. and Sethian, J.A. An o(n log(n)) Algorithm for Shape
Modeling. Applied Mathematics 18:9389-9392, 1996.
[3] Taubin, G. A Signal Processing Approach to Fair Surface Design.
Computer Graphics, 29:351-358, 1995.
[4] Wang, K. and Wang, Y. Alignment of Curves by Dynamic Time Warping.
Annals of Statistics, 25:1251-1276, 1997.
[5] Witelson, S.F. Hand and sex differences in the isthmus and genu of
the human corpus callosum. Brain 112:799-835. 1989.
|
|
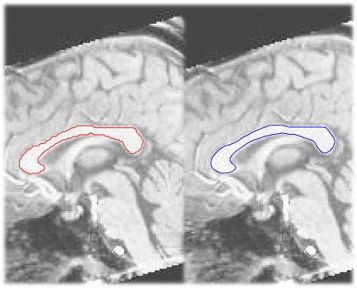
Figure 1. Leveset segmentation and smoothing
|
|
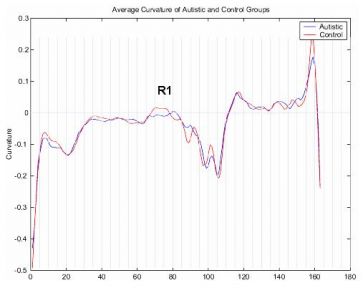
Figure 2. Mean curvatures for autism and
control
|
|
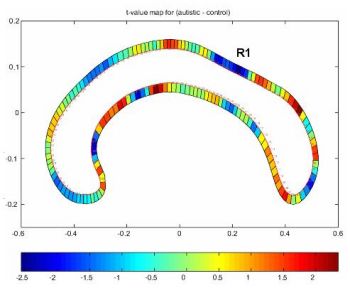
Figure 3. t-map of curvature difference
between autism and control
|
|
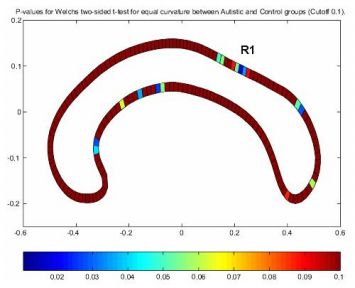
Figure 4. p-map of curvature difference
|
|
|