Description
January 8, 2008
Using the
weighed
spherical harmonic (SPHARM) representation
[1], amydala surface will be parameterized and quantified in a two
group comparision setting. The implementation is based on MATLAB 7.5
and a Mac-Intel computer.
Loading T1-weighted Analyze images into MATLAB
January 8, 2008
lefthdr =
/Users/chung/Desktop/amygdala/study1/subject001/Tracing_mask_left.hdr
/Users/chung/Desktop/amygdala/study1/subject002/Tracing_mask_left.hdr
/Users/chung/Desktop/amygdala/study1/subject005/Tracing_mask_left.hdr
.....
To load the left amygdala of subject 001 (header, image) we run
>leftinfo = analyze75info(lefthdr(1,:));
The above
line reads the header information (*.hdr). To find out the image
dimension, we run
>>
leftinfo.Dimensions
ans =
191 236
171 1
From Figure 1, we see that Saggital 191 x
Coronal 236 x Axial 171. The last numer 1 indiates that this header
file is incorretly constructed. ;) To read *.img, we run
>vol = analyze75read(leftinfo);
Using the marching cubes algorithm, we segment the amydala surface as a triangle mesh:
>surf = isosurface(vol)
surf =
Figure 1. The coordinates directly
correspond to the voxel positions of Tracing_mask_left.img. Right
figure is generated using MRIcro.
Amygdala Surface Flattening
January 20, 2008
The surface flattening from an
amygdala surface to a unit sphere is needed for establishing a
parameterization on the amygdala surface [1]. We have developed a novel
flattening techniue using heat diffusion. We first enclose the amygdala
binary mask with a larger sphere (Figure
2 left). Take the amygadala as a source (value +1) and the
sphere as a sink (value -1).
>[amyg,sphere,amygsphere]=CREATEenclosedamyg(vol,surf);
>figure;imagesc(squeeze(amygsphere(:,25,:)));colorbar
With the
heat sink and source, we perform isotropic heat
diffusion for long time. After suffiient amount of time, we
reach a stady state, which is equivalent to solving the Laplace quation.
The following code will run approximately 5 min. per surface.
>stream=LAPLACE3Dsmooth(amygsphere,amyg,-sphere);
>figure;imagesc(squeeze(stream(:,25,:)));colorbar
The result
is given in Figure 2.
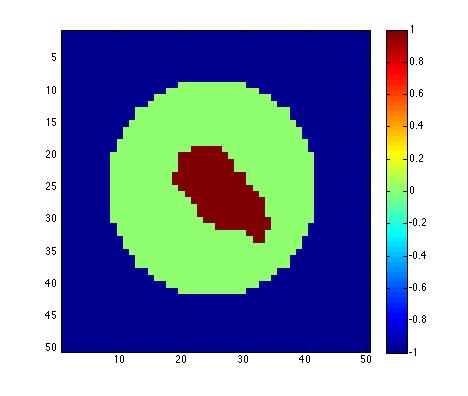
Figure 2. Left: amygdala is asigned
the value 1 and the sphere enclosing the amydala is asigned the value
-1. Right: After solving isotropic heat diffusion for long time, we
reach a statedy state, which can be used to generate a mapping from the
amygdala surface to the sphere by taking the geodesic path
from value 1
to -1.
The stady state map (Figure 2) is used to generate a mapping from the amygdala surface to the sphere. This is done by computing the geodesic path from the source to the sink. We first compute the levet sets of the stady state corresponding to f(p) = c for -1 <= c <=1 and propagate the amygdala boundary (c=1.0 in Figure 3) to the next level set (c=0.6) by computing the geodesic path. The propagation from one level set to the next is done by LAPLACEcontour. The flattening process is expected to produce discretization error. For each level set, we regularize mesh by shrinking down larger than expected area of triangles using REGULARIZEarea. 20% of the larger than expected triangles are reduced in size by setting the parameter to 0.8 in REGULARIZEarea.
>sphere=isosurface(amyg);
>for alpha=1:5
> sphere=LAPLACEcontour(stream,sphere,
1 - 2*alpha/5);
> sphere=REGULARIZEarea(sphere,
0.8);
> figure_wire(sphere,'yellow')
>end;
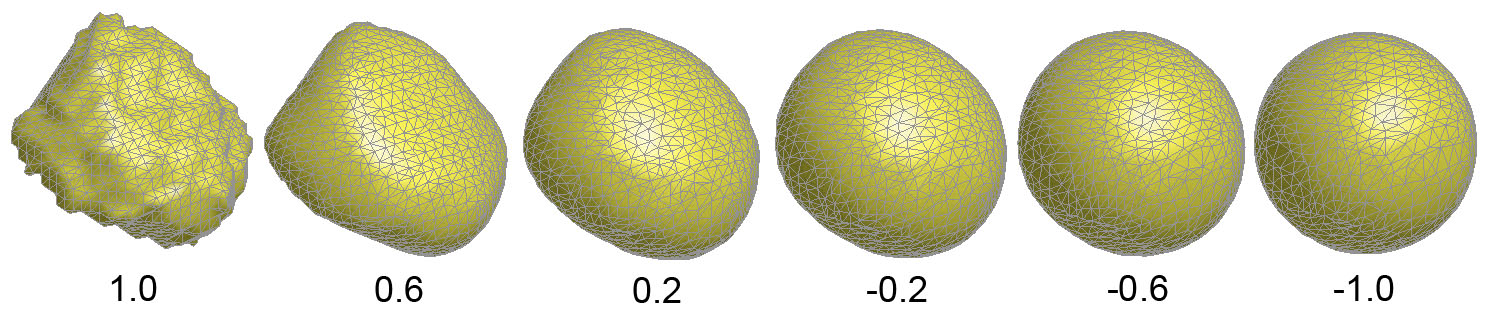
Figure 3. Amygdala surface
flattening process using the geodesic path of of the stady state map.
The parameters correspond to the level set f(p)=1.0, 0.6, ..., -0.6,
-1.0.
Weighted Spherical Harmonic Representation
January 22, 2008
Once
we establish the mapping from the amygdala surface onto a sphere, we
can determine the Euler angles
\theta and \varphi. The domain of \theta and \varphi in this
study follows the convention established in [1], which is different
from the result directly obtained from cart2sph.m. Continuing directly
from the above for-end loop, we run
>[theta
varphi]=EULERangles(surf);
>surf=isosurface(amyg);
>figure_trimesh(surf,theta)
>figure_trimesh(surf,varphi)
figure_trimesh
projects Euler angles \theta and \varphi to the amygdala surface (Figure 4). The Euler angles are
necessary to establish the weighted spherical
harmonic representation
on a unit sphere. The additional MATLAB implementation details on the
weighted spherical harmonic representation can be found here.
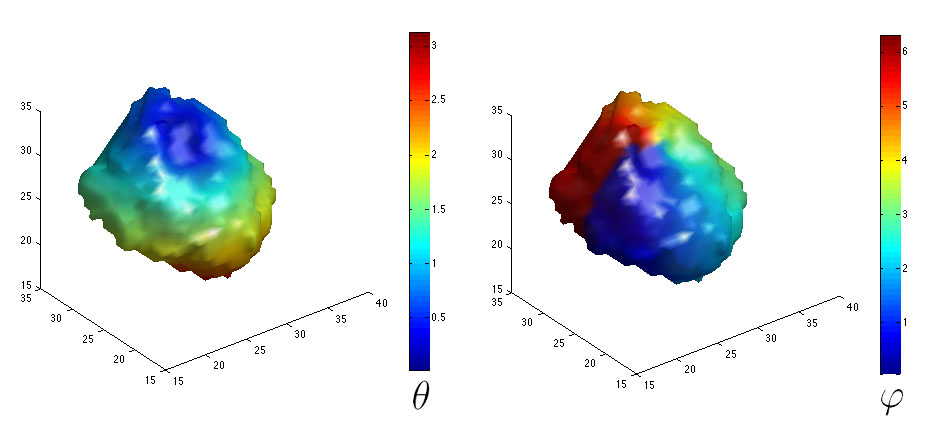
Figure 4. Euler angles projected
onto an amygdala surface. North pole is taken where \theta=0 (blue peak
in the left figure).
The
weighted spherical harmonic representation of degree 60 and bandwidth
sigma=0 is given by running the code
>[surf_smooth,
fourier]=SPHARMsmooth2(surf,sphere,60,0);
>figure_wire(surf_smooth,'yellow')
where
surf is the amygdala surface and sphere is the spherical mesh obtained
by running LAPLACEcontour
and REGULARIZEarea. When the bandwidth is zero, the
weighted spherical harmonic representation becomes the traditional
spherical harmonic representation. See refernce [1] and [2] for detail.
Figure 5 shows various degree
representation.
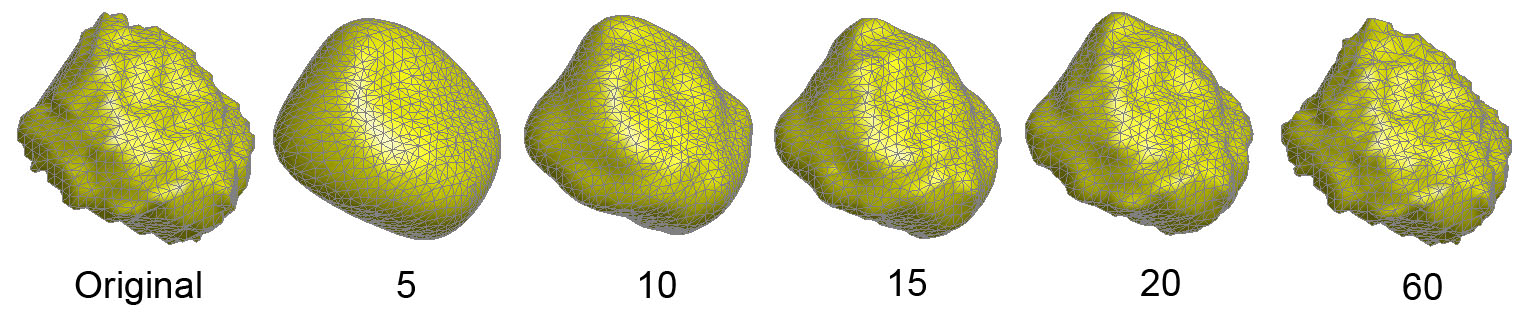
Figure 5. Spherical harmonic
representations of a left amygdala surface. Degree 15 will be chosen
for subsequent statistical analysis.
Gibbs Phenomenon (Ringing Artifacts)
January 23, 2008
The Fourier series are known to
introduce the Gibbs
phenomeon (ringing artifacts) [1}. The Gibbs phoenomeon occurs
near rapidgly changing or discontinous measurments. Since the
spherical harmonics are continuous and smooth basis functions, it is
not possible to represent discontinuity of data using spherical
harmonics.
Figure 6. The Gibbs phenomeon is
particuarly visible in the SPHARM representation with k=42 and
\sigma=0. The ringing artifact is reduced if we introduce a bit of
smoothing \sigma=0.001.
Saving and Loading multiple surfaces
January 30,
2008
The
following line of codes will process a surface corresponding to subject
id(i,:) and save the results into a seperate *.mat file.
>for
i=1:size(id,1)
> %put surface flattening + weighted spherical
harmonic modeling here
> id_write=strcat('study1.right.',id(i,:),'.mat');
> save(id_write,'fourier');
>end
We can load *.mat files iteratively and save them into a structrued array study1_left:
>for
i=1:size(id,1)
> file_name=strcat('study1.left.',id1(i,:),'.mat');
> load(file_name);
> study_left(i,:)=fourier;
>end;
The
Fourier coefficinets of the 10th-subject is given by
> study_left(10,:)
ans =
x: [43x85 double]
y: [43x85 double]
z: [43x85 double]
Constructing Average Amygdala Template
January 30,
2008
The average amygdala surfaces are
constructed by averaging the collection of Fourier coefficients up to
degree 15.
>load unitsphere2562.mat
%this load unit sphere surface mesh with 2562 vertices
>left_average=SPHARMaverage(study_left,sphere,
15,0.01);
>figure_patch(left_average,'yellow');
>right_average=SPHARMaverage(study_right,sphere,
15,0.01);
>figure_patch(right_average,'yellow');
The parameters 0.01 introduce a
little bit of smoothing into the representation.
Figure 7. The average left and right
amygdala surfaces over 47 subjects (24 control and 23 autistic
subjects).
Deformation-Based Morphometry
January 30, 2008
From
study_left and study_right that contains Fourier coefficients, we
constructed the weighted spherical
harmonics with degree 15 and bandwidth sigma 0.01. The
resulting coordinates are stored as matrix left_surf and right_surf.
left_surf=zeros(2562,3,47);
right_surf=zeros(2562,3,47);
for i=1:47
temp=SPHARMrepresent2(sphere,study_left(i),15,0.01);
left_surf(:,:,i)=temp.vertices;
temp=SPHARMrepresent2(sphere,study_right(i),15,0.01);
right_surf(:,:,i)=temp.vertices;
end;
We
seperate surfaces into two groups (control vs. autistic). The group
variable is denoted as a binary number (control=0, autistic = 1):
group=
[zeros(12,1); ones(13,1); zeros(12,1);
ones(10,1)]
left_c=left_surf(:,:,find(~group));
left_a=left_surf(:,:,find(group));
right_c=right_surf(:,:,find(~group));
right_a=right_surf(:,:,find(group));
left_c
contails all surface coordinates for control subjects while left_a
contains all surface coordinates for autistic subjects. Then
the
Hotelling's
T-square statistic is used to measure the discrepancy
between autistic and control amygdala surfaces.
[h p]=hotelT2(left_c,left_a);
h
is the Hotelling's T-square statistic and p is the corresponding
P-value.
figure_hotelT2(left_c,left_a,0.1,sphere);
Figure 8. The P-value of testing the
significance of group difference projected on to the mean control
surface. Thw white arrows indicates where to move the the mean control
surface to match
it to the mean autistic surface.
Amygdala Volumetry
Febuary 3, 2008
The
traditional amygdala volumetry can also be done. Make sure
that vol only contains value 1 or 0 otherwise, the following code
will not work.
for
i=1:size(id,1)
rightinfo = analyze75info(righthdr(i,:));
vol = analyze75read(rightinfo);
leftvol(i)=sum(sum(sum(vol)));
rightvol(i)=sum(sum(sum(vol)));
end;
save volumetry.mat left_vol right_vol
load volumetry
al= left_vol(find(group))
ar=right_vol(find(group))
cl= left_vol(find(~group))
cr=right_vol(find(~group))
[mean(al) std(al)]
[mean(ar) std(ar)]
[mean(cl) std(cl)]
[mean(cr) std(cr)]
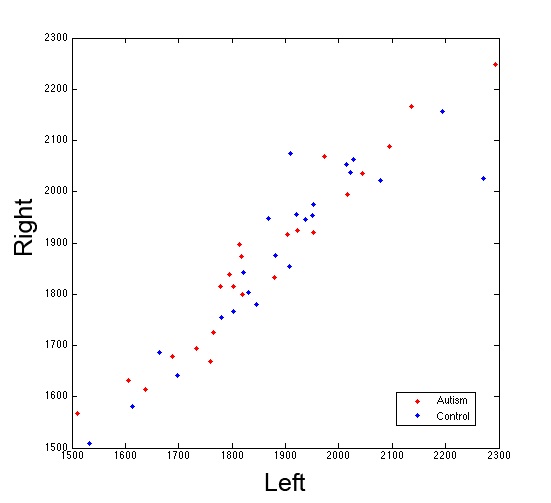
plot(al,ar,'.r')
hold on
plot(cl,cr,'.b')
legend('Autism','Control')
%two
sample t-test on amygala volume
[h,p] = ttest2(al,cl)
[h,p] = ttest2(ar,cr)
References
January
6, 2008