Project Description
The twin study design offers a
very effective way of determining the heritability
of the human brain. The difference in variability
between monozygotic and same-sex dizygotic twins
can be used to determine the heritability of an
imaging-based phenotype at each voxel. Except for
few well known neural circuits, the extent to
which heritability influences the brain network is
not well established. Compared to many existing
studies on univariate phenotypes in brain imaging,
there are not many studies on the heritability of
brain networks. Measures of network topology and
features may be worth investigating as
intermediate phenotypes or endophenotypes.
However, the existing brain network analysis has
not yet been adapted for this purpose. Determining
the extent of heritability of brain networks with
large number of nodes is the first necessary
prerequisite for identifying network-based
endophenotypes. This requires constructing the
large-scale brain networks by taking every voxel
in the brain as network nodes with at least a
billion connections, which is a serious
computational bottleneck. We propose to map the
heritability of large-scale brain networks by
taking every voxel in images as network nodes
using persistent homology and sparse
network models (Figure 1,2). By exploiting
the topological structure of data, we can show
that it is possible to bypass the bottleneck and
learn networks with billion connections without
much computational resource such as cluster
computing.
Matlab Codes
The exact topological inference procedure is packaged into a zipped file: matlab.2017.IPMI.zip. The package will run two simulation studies given in Chung et al. (2017, IPMI). It contains codes for computing probability given in Theorem 2 and 3 as well as codes for computing Kolmogorove-Smirnov (KS) and Gromov-Housdorff (GH) distance for networks. The exact topological inference is limited to integer-valued monotone features without any gap between consecutive integer values.The sparse hyper-network construction is done via soft-thresholding as explained in Chung et al. (2017). Soft-thresholding based sparse network construction is first explained in Chung et al. (2015, IEEE TMI). The procedure is packaged into a single zipped file: hyper-network.zip, where a toy example is used as an illustration for how the method works.
The heritability index of the constructed sparse hyper-network at the network level is also given: heritability-network.zip. Start heritability-network.m in the zipped file to construct the dense network with more than 5000o nodes. You need large computer RAM memory to even construct and visualize dense connections.
The exact combinatorial inference generalizes the exact topological inference to any arbitrary monotone features. They don't have to be consecutive integer values. The method is published in Chung et al. (2018, MICCAI) and MATLAB codes are packaged into a zipped file: matlab.2018.MICCAI.zip.
The performance of KS-distance against GH-distance and other matrix norm based distances are given in matlab.2017.CNI.zip. The package will run multiple simulation studies given in Chung et al. (2017).
Exact topological inference can be done to Betti-1 number (the number of cycles). The number of cycles can be computed from Betti-0 number. The detail is given in Chung et al. (2018). The MATLAB codes for computing Betti-1 plots and simulations done in the paper is given in matlab.2018.NN.zip.
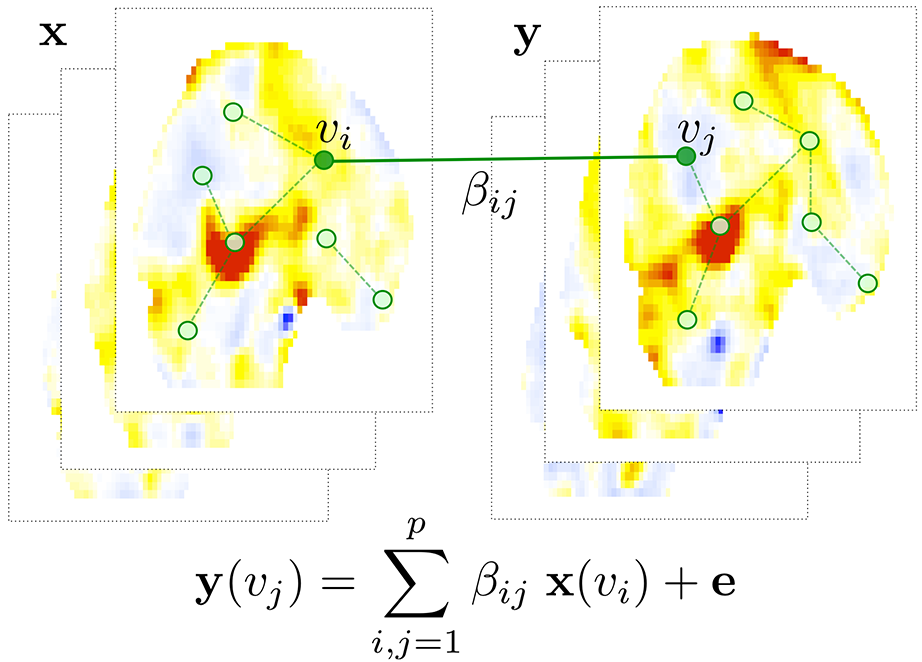
Figure 1. The schematic of hyper-network construction on twin image vectors. The second pair of images y is modeled as a linear combination of the first pair of images x. The estimated weights of the linear combination gives the hyper-edge weights. See [3] for detail.
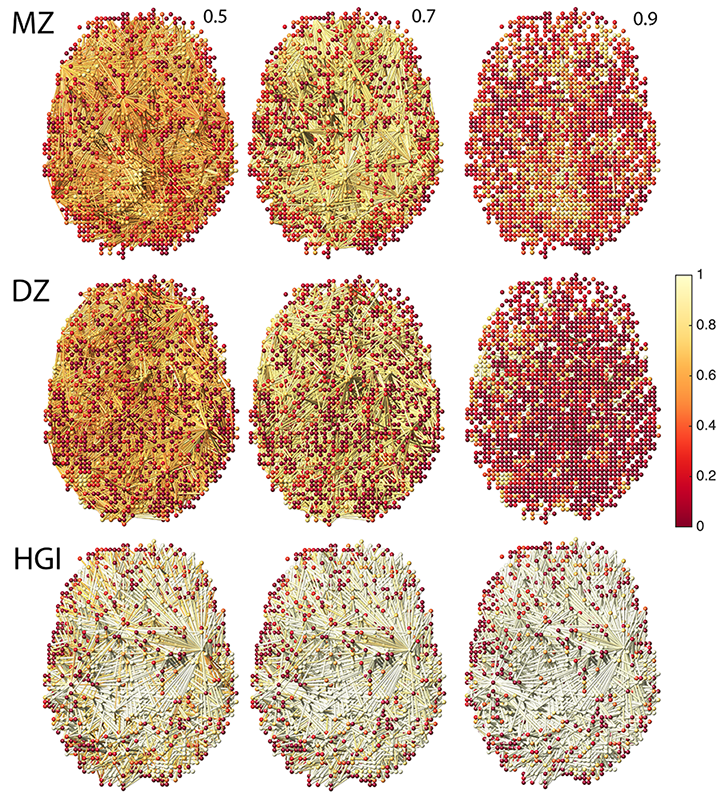
Figure 2. Estimated hyper-networks at three different sparse parameters 0.5, 0.7 and 0.9 for MZ- and DZ-twins. As the sparse parameter increases, we have more sparse hyper-connections. HGI measures heritability index at the nodes and along the hyper-edges. See [3] for detail.
Publication from the Project
[1] Chung,
M.K., Vilalta, V.G., Rathouz, P.J., Lahey, B.B.,
Zald, D.H. 2016 Heritability
of large-scale functional brain networks.
Organization for Human Brain Mapping (OHBM) (invited talk)
Lecture
slides, Poster[2] Chung, M.K., Vilalta, V.G., Rathouz, P.J., Lahey, B.B., Zald, D.H. 2017 Hyper network analysis on paired images. International Society of Magnetic Resonance in Medicine (ISMRM) (accepted for oral)
[3] Chung, M.K., Vilalta, V.G., Lee, H., Rathouz, P.J., Lahey, B.B., Zald, D.H. 2017 Exact topological inference for paired brain networks via persistent homology. Information Processing in Medical Imaging (IPMI) (accepted for oral) MATLAB arXiv:1509.04771
[4] Chung, M.K., Lee, H., Solo, V., Davidson, R.J., Pollak, S.D. 2017 Topological distances between brain networks, International Workshop on Connectomics in NeuroImaging, Lecture Notes in Computer Science, in press. (plenary talk) Extended version arXiv:1701.04171 MATLAB
[5] Chung, M.K. 2018 Statistical challenges of big brain network data, Statistics & Probability Letters 136:78-82 (invited paper) arXiv:1709:09645
[6] Chung, M.K., Luo, Z., Adluru, A., Alexander, A.L., Richard, D.J., Goldsmith, H.H. 2018 Heritability of hierarchical structural brain network. IEEE Engineering in Medicine and Biology Society (EMBC) doi.org/10.1101/209635, in press
[7] Chung, M.K., Luo, Z., Adluru, A., Alexander, A.L., Richard, D.J., Goldsmith, H.H. 2018 Exact Combinatorial Inference for Brain Images, Medical Image Computing and Computer Assisted Intervention (MICCAI), in press