Description
July 17, 2020Diffusion tensor imaging (DTI) provides the directional information of water molecule diffusion in the white matter fibers of the human brain. It is usually represented as the collection of 6 multivariate images that represent a 3 by 3 symmetric positive definite matrix called diffusion coefficients or diffusion tensors. The diffusion coefficients can be used to understand the pattern of white fibers in the brain.
Kernel smoothing in DTI
DTI often requires
spatial smoothing to reduce noise. Most previous
regularization works on diffusion tensor magnetic
resonance images have been based on either
anisotropic heat equations or streamline approaches.
We developed a novel regularization method using
iterated anisotropic kernels that avoids solving
diffusion equations or streamline equations while
improves upon numerical stability (Chung et al.
2003, Lee et al. 2005). The bandwidth of kernel is
proportionally matched to the diffusion tensor to
smooth out more along the tensor fields (Figure 1).
The proportionally constant is chosen to minimize
the sum of the squared intensity
difference between before and after smoothing while maximizing
the smoothness of the image. The kernel method can
be shown to increases the signal-to-noise ratio
while preserving the anisotropy of the tensor
fields. This formulation can be shown to be
equivalent to the edge enhancing diffusion equation
approaches. 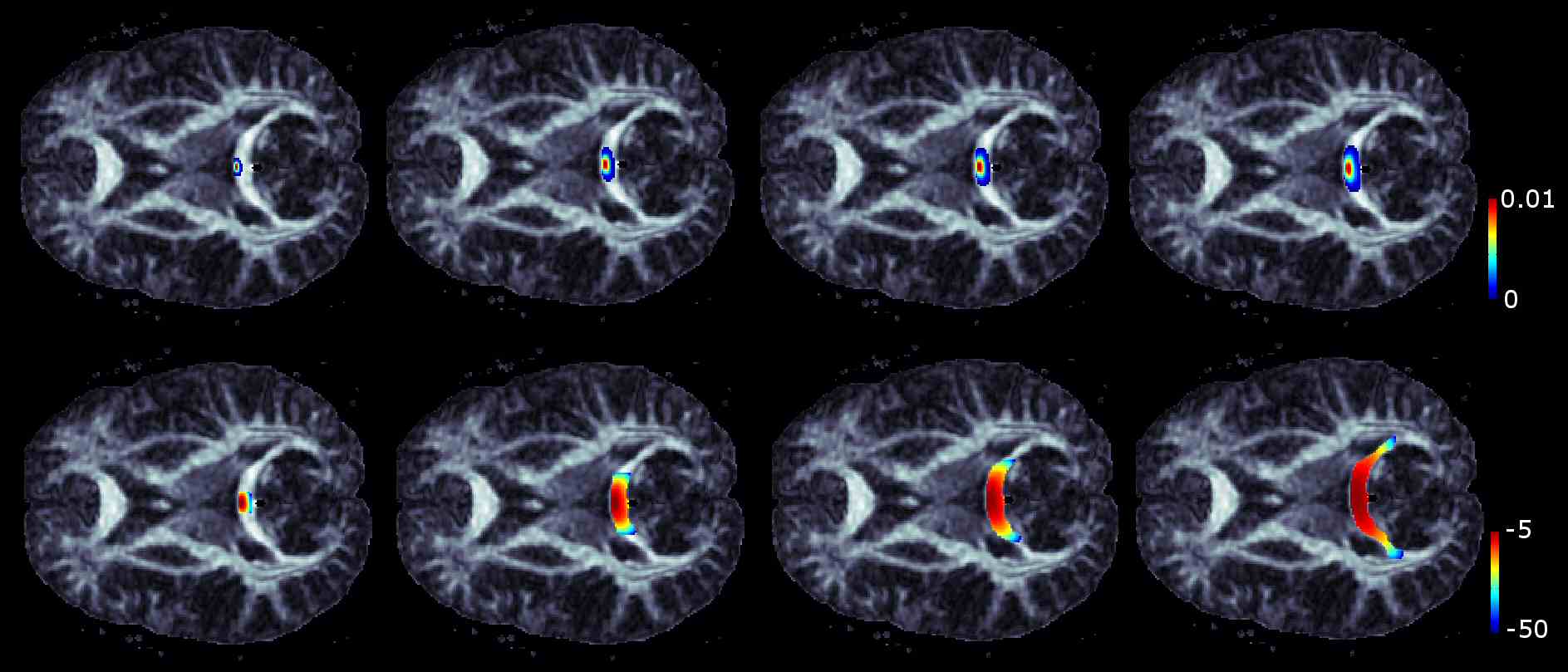
Figure 1. Probabilistic connectivity obtained by iterated heat kernel smoothing
Structural connectivity
Streamline
based tractography is often used in determining
the connectivity between brain regions. In Chung
et al. 2019, 10
million tracts were extracted then biologically
informed 1 million tracts were extracted. Figures
2 and 4 show the average connectivity of males and
females (reproduced from Figure 3 in Chung
et al. 2019). The average connectivity
matrices and t-stat map used in producing Figure 2
are stored as MAT file: chung.2019.CNI.mat.
The MAT file contains the sample mean of female
(mean(x)), the sample mean of males(mean(y)), the
sample variance of females (var(x), the sample
variance of males (var(y)). It also contains the
t-stat of sex difference computed as (mean(x)-mean(y)).*sqrt(m*n*(m+n-2)./((m+n)*((m-1)*var(x)+(n-1)*var(y))));
The MAT file also contains the t-stat pooling the two groups (Figure 3) computed as
(mean(x)+mean(y)).*sqrt(m*n*(m+n-2)./((m+n)*((m-1)*var(x)+(n-1)*var(y))));
Here m and n are the sample size in females and males respectively.
Notice: If you use MAT file for whatever purpose, please reference Chung et al. 2019 [1].
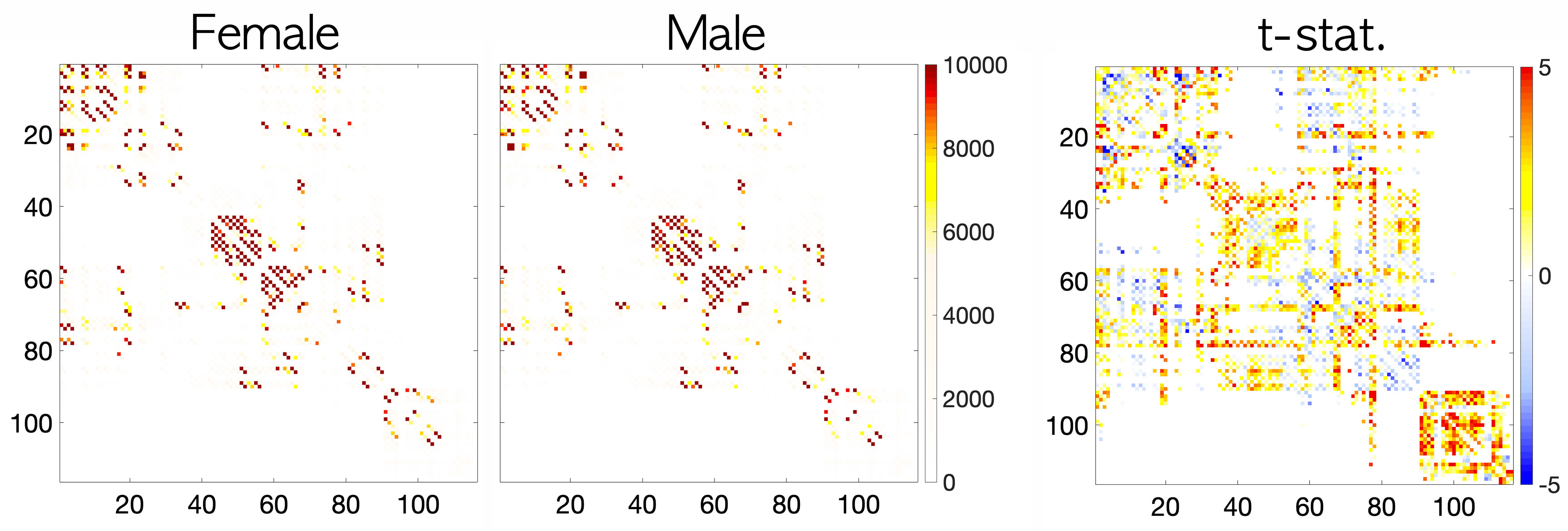
Figure 2. Average connectivity matrices of females (left) and males (right) between 116 AAL parcellations. The two-sample t-statistic result (female − male). Females have more structural connections between brain regions than males.
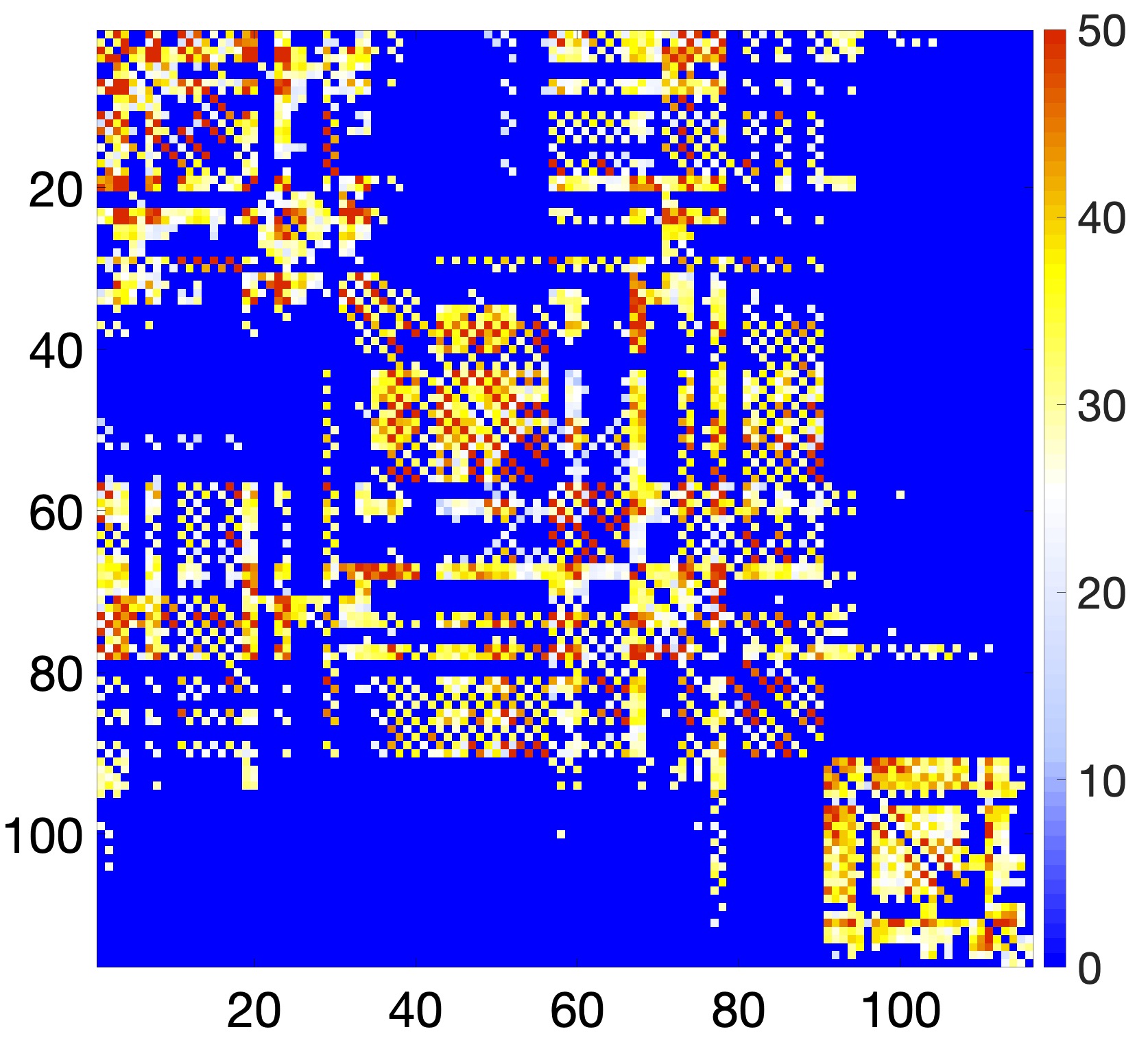
Figure 3. t-stat on combined sample of female and male. This is the average connectivity of whole population (female and male combined) that account for group variability difference. This connectivity map can be used as a prior structural information, where functional connectivity can be overlaid somehow.
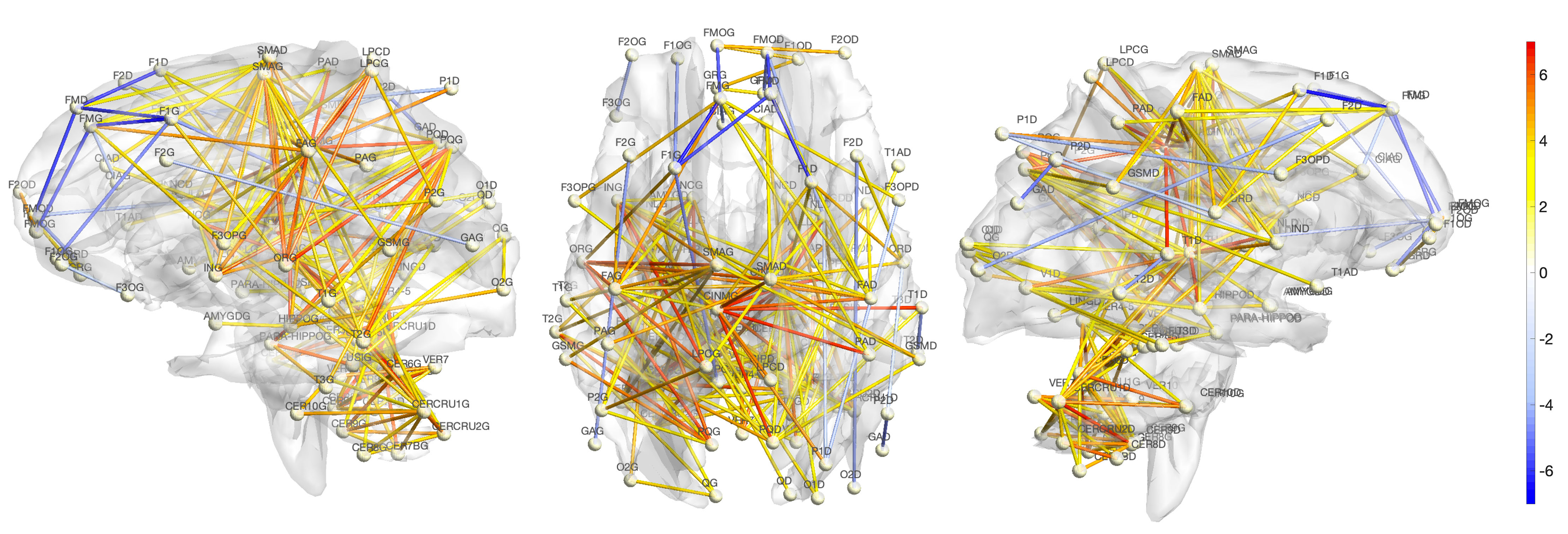
Figure 4. The t-stat map in Figure 2 was used to construct 3D graph representation of network differences. Only the connections that are statistically significant (thresholded at −4.05 and 3.96) after multiple comparisons correction at 0.05 are shown. Females have more connections in most parts of the brain while males are more connected in the frontal regions of the brain.
Reference
[1] Chung, M.K., Xie, L, Huang, S.-G., Wang, Y., Yan, J., Shen, L. 2019 Rapid acceleration of the permutation test via transpositions, International Workshop on Connectomics in NeuroImaging, Lecture Notes in Computer Science (LNCS) 11848:42-53. An earlier version with different application arXiv:1812.06696
- [2] Lee, J.E. Chung, M.K., Hsu, D., Alexander, A.L. 2007. Probabilistic connectivity using Kullback-Leibler distance, International Socieity for Magnetic Resonance in Medicine (ISMRM) conference. Poster
- [3] Lee, J.E., Chung, M.K., Alexander, A.L. 2006. Evaluation of anisotropic filters for diffusion tensor imaging. IEEE International Symposium on Biomedical Imaging (ISBI) 1241
- [4] Lee, J.E., Chung, M.K., Alexander, A.L. 2006. Evaluation of anisotropic filtering for DTI as a function of SNR. Proceedings of the 14th ISMRM Scientific meeting.
- [5] Lee, J.H., Chung, M.K., Oakes, T.E., Alexander, A.L. 2005. Anisotropic Gaussian kernel smoothing of DTI data. 13th Meeting of International Society for Magnetic Resonance in Medicine. 2253.
- [6] Chung, M.K., Lazar, M., Alexander, A.L., Lu., Y., Davidson, R. 2003. Probabilistic Connectivity Measure in Diffusion Tensor Imaging via Anisotropic Kernel Smoothing, Technical Report 1081. Department of Statististics, Universisty of Wisconsin-Madison.
- [7] Chung, M.K., Alexander, A.L., Lu, Y. 2003. Connection Probability in Diffusion Tensor Imaging via Anisotropic Gaussian Kernel Smoothing, 9th Annual Meeting of the Organization for Human Brain Mapping.