Description

Dynamic topological data analysis (dynamic-TDA)  focuses on analyzing dynamically changing time series data using persistent homology. The method can be applicable to wide variety of dynamically changing data including resting-state functional magnetic resonance images (rs-fMRI) and dynamically changing correlation matrices. The basic terminology and concept are introduced in [1]. If you use data or codes in this page, please reference Songdechakraiwut et al. 2020. Codes below explained in section 1)-3) are packaged as song.2020.simulation3.zip. Section 1)-3) perform the transposition test topological distance on the two-groups setting. Simply run run_simulation_v3.m.

1) Modular network simulation

This is the basic statistical model given as Study 2 in the simulation study in Songdechakraiwut et al. 2020. Function random_modular_graph.m will generate a modular network. The input parameters are as follows.

mu = 1;                  %mean
sigma = .25;         %standard deviation
nNode1 = 50;       %number of nodes in network G
nModule1 = 2;     %number of modules of graph G
nNode2 = 60;       %number of nodes in network P
nModule2 = 3;     %number of modules of graph P
nModule2 = 3;     %number of modules of graph P

G = random_modular_graph(nNode1, nModule1, p, mu, sigma); %network with 2 modules
P = random_modular_graph(nNode2, nModule2, p, mu, sigma); %network with 3 modules
figure; subplot(1,2,1); imagesc(G); colorbar
subplot(1,2,2); imagesc(P); colorbar

 

Figure 1. Simulated networks with 2 modules and 3 modules. The parameter p controls the probability of connection within the module. 

The graphs can be displayed by thresholding the complete graph at 0.5 and displaying them as binary graphs:

Gbinary = adj2bin(G,0.5);
Ggraph = graph(Gbinary)

2) Wasserstein distance on graphs

 The Wasserstein distance between two graphs of different size and topology is first introduced in Songdechakraiwut et al. 2020. WS_distance.m computes the sum of 0D and 1D Wasserstein distance between two weighted adjacency matrices G and P. 

>WS_distance(G,P)
ans =
   19.9532

WS_distancemat.m computes the topological loss between groups and within groups and represent it as a loss matrix. We will generate two groups. The first group g1 will have 4 networks with 2 modules. The second group g2 will have 6 networks with 3 modules. Since they are topologically different,

nGroup1 = 4;
nGroup2 = 6;
g1 = cell(nGroup1, 1);
g2 = cell(nGroup2, 1);
for k = 1:nGroup1
    g1{k} = random_modular_graph(nNode1, nModule1, p, mu, sigma);
end
for k = 1:nGroup2
    g2{k} = random_modular_graph(nNode2, nModule2, p, mu, sigma);
end

lossMtx = WS_distancemat('top', g1, g2, []);
figure; imagesc(lossMtx); colorbar


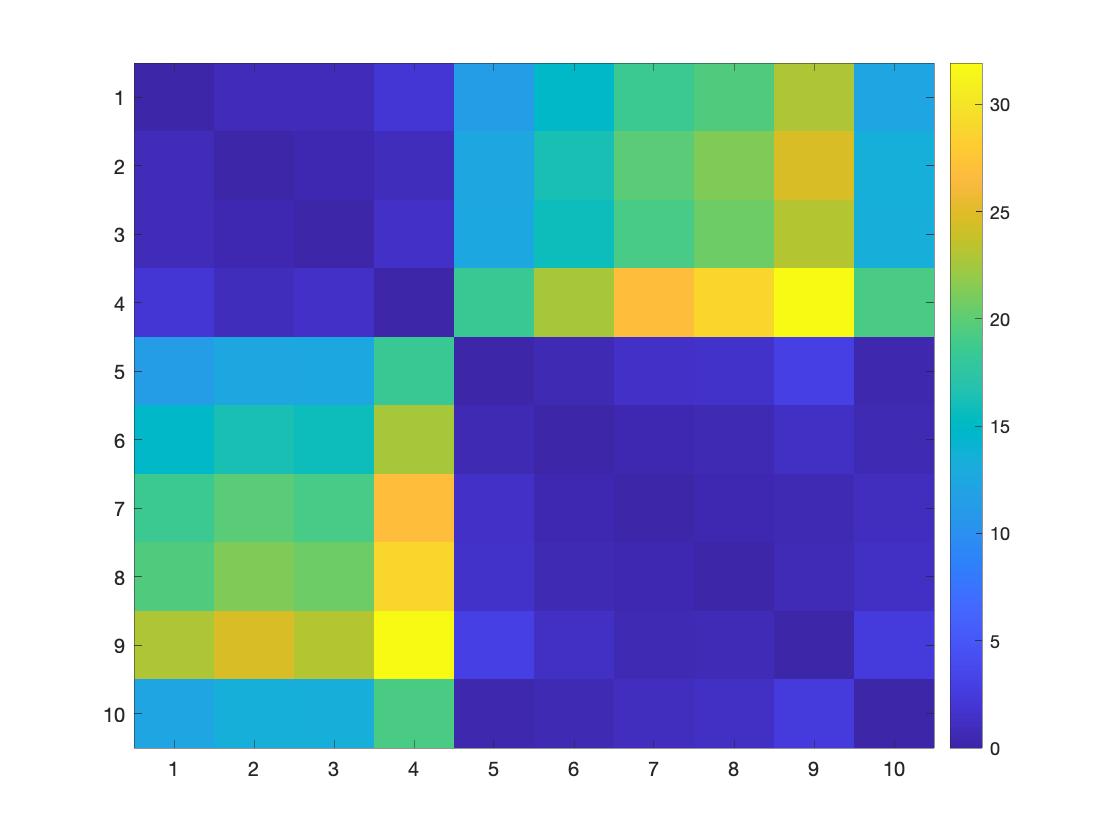
Figure 2. The topological loss within groups is lower than the topological loss between groups.

3) Topological inference on Wasserstein distance via transpositions

The transposition test on the ratio statistic of thee  between-group loss over within-group loss is computed as follows (study 2 in Songdechakraiwut et al. 2020). An additional weblink for the transposition test is given here.

observed = WS_ratio(lossMtx, nGroup1, nGroup2, @between_over_within)
nTrans = 200000;                      % number of transpositions
permNo = 500;                           % intermix random permutation every 'permNo' transpositions
[transStat, ~] =WS_transpostions(lossMtx, nGroup1, nGroup2, nTrans, permNo, @between_over_within);
transPval = online_pvalues(transStat, observed);
pval = transPval(end)

4) Wasserstein clustering on graphs

Figure 1 already shows clustering pattern indicating the Wasserstein distance can be used in clustering graphs and networks. We can show that the clustering using the Wasserstein distance is equivalent to k-means clustering in a convex domain. Clustering is performed on a different dataset and packaged into matlab-WassersteinClustering.zip. The method is published in [8]. The clustering accuracy is computed using clustering_accuracy.m which performs the linear sum assignment problem on the confusion matrix. The detail is given here.

Reference

[1] Songdechakraiwut, T. Chung, M.K. 2020 Dynamic topological data analysis for functional brain signals, IEEE International Symposium on Biomedical Imaging (ISBI) Workshop 1-4  Shorter abstract

[2] Songdechakraiwut, T. Chung, M.K. 2020 Topological learning for brain networks, arXiv: 2012.00675

[3] Chung, M.K., Huang, S.-G., Songdechakraiwut, T., Carroll, I.C., Goldsmith, H.H. 2020 Statistical analysis of dynamic functional brain networks in twins, arXiv 1911.02731  MATLAB

[4]  Kulkarni, A.P., Chung, M.K., Bendlin, B.B., Prabhakaran, V. 2020 Investigating heritability across resting state brain networks via heat kernel smoothing on persistence diagrams,  IEEE International Symposium on Biomedical Imaging (ISBI) workshop 1-4.

[5] Huang, S.G., Chung, M.K., Qiu, A, ADN Initiative 2020 Revisiting convolutional neural network on graphs with polynomial approximations of Laplace-Beltrami spectral filtering, arXiv:2010.1326

[6] Huang, S.G., Chung, M.K., Qiu, A, ADN Initiative 2020 Fast mesh data augmentation via Chebyshev polynomial of spectral filtering, arXiv:2010.02811

[7] Chung, M.K., Xie, L., Huang, S.-G., Wang, Y., Yan, J., Shen, L. 2019. Rapid Acceleration of the permutation test via transpositions, International Workshop on Connectomics in NeuroImaging, Lecture Notes in Computer Science 11848:42-53. A different version arXiv:1812.06696

[8]  Anand, D.V., Dakurah, S., Wang, B., Chung, M.K. 2021 Hodge-Laplacian of brain networks and its application to modeling cycles. arXiv:2110.14599